摘要
由于相位和結構之間的直接關系,衍射分束鏡通常采用一定的傍軸近似來設計,這些算法也提供了這種近似,反之亦然。在非傍軸或甚至高NA分束器的情況下,這些近似將引入一些不準確性,因此,如果不進行額外嚴格的后優化,至少建議進行嚴格的分析。在這個用例中,使用奇數衍射級對典型的二元1:6分束器執行這樣嚴格的評估。為此,對初始系統的結構進行了參數化,并通過可編程光柵分析器定義了一組自定義的評價函數。對于參數優化和后續的公差分析,使用嚴格的傅里葉模態法 (FMM)。
建模任務
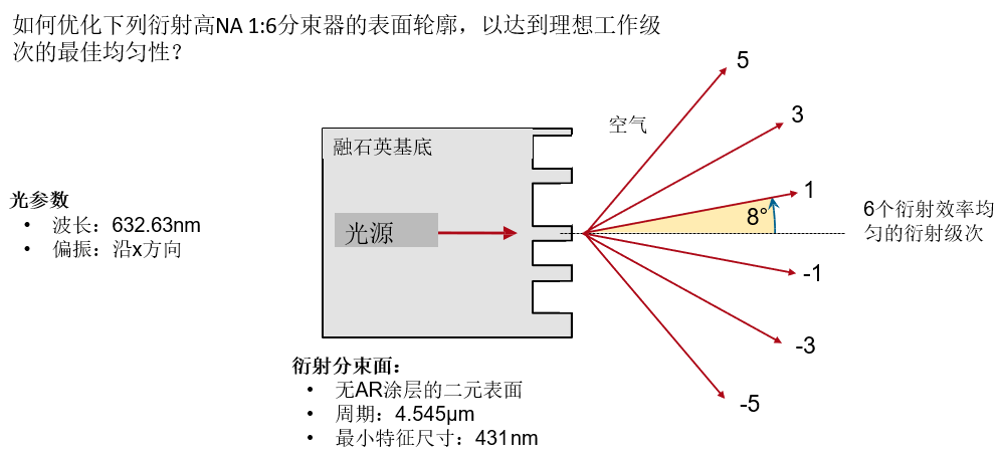
衍射分束面初始設計(*)
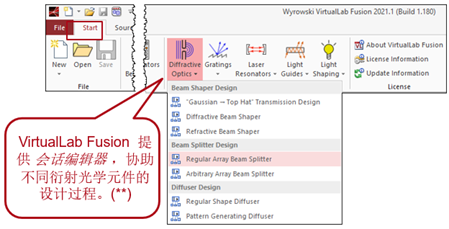
1. 采用VirtualLab Fusion的迭代傅里葉變換算法(IFTA)設計工具計算了分束器的初始相位函數。
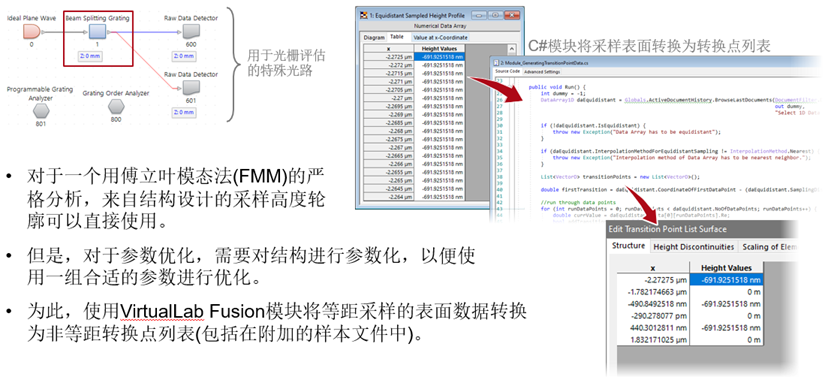
2. 對于高度輪廓的轉換,采用了基于薄元件近似(TEA)的結構設計。
(*)不是這個用例的一部分 (**)這些會話編輯器在衍射光學工具箱銀版中可用。
TEA和等距抽樣結構的局限性
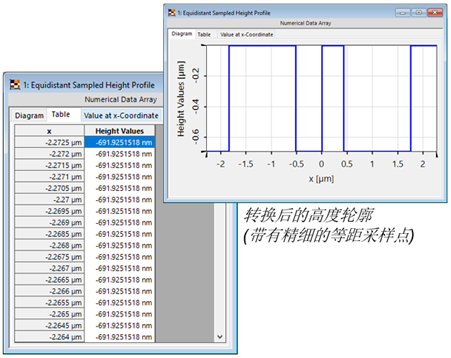
TEA非常適合于最小特征尺寸不小于約5倍波長的情況。如果不是這樣,振幅/相位分布與設計高度輪廓相互作用后可能會顯示出與期望值的相關偏差。
因此,需要進行嚴格的評估。
對于參數優化,需要對結構數據進行不同的定義。
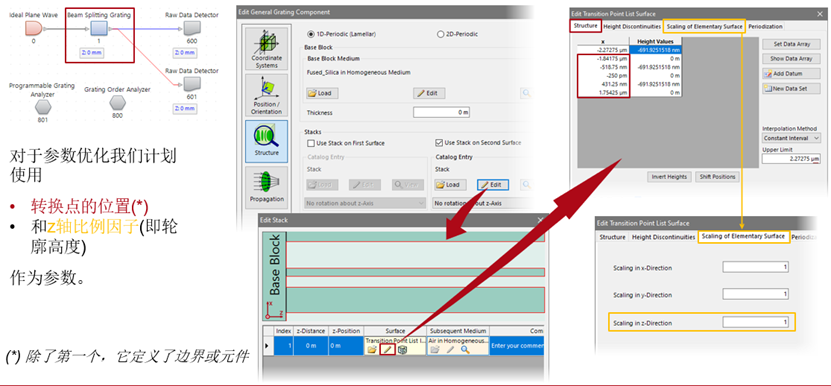
后優化的數據準備(參數化)
衍射分束器表面進一步優化
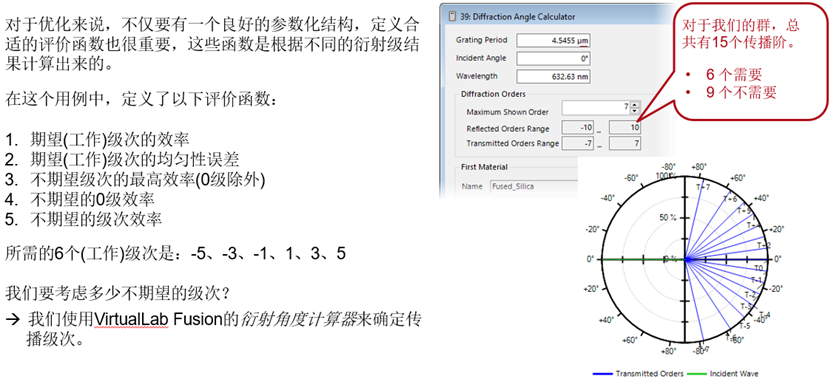
哪個衍射級次有哪些評價函數?
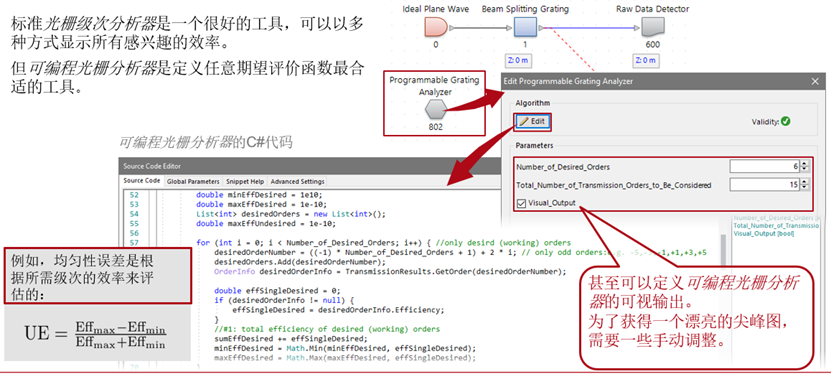
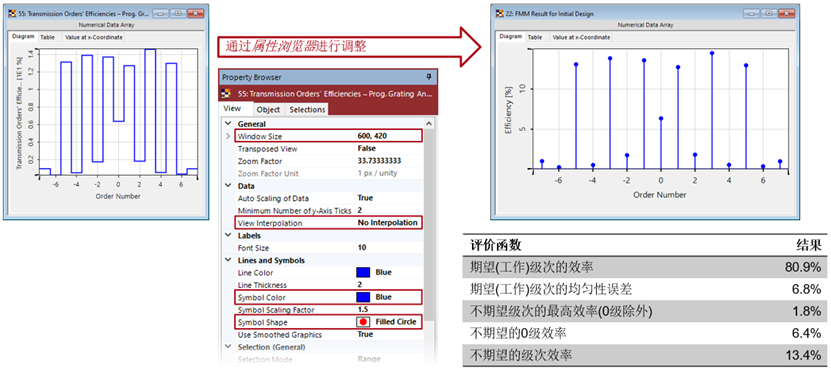
利用可編程光柵分析器
分束器初始設計的嚴格分析
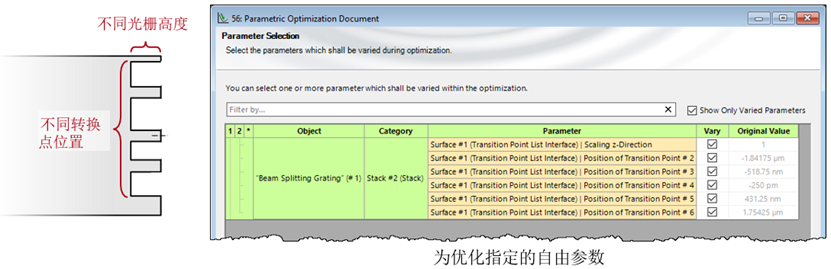
設置優化參數
兩個優化過程對比
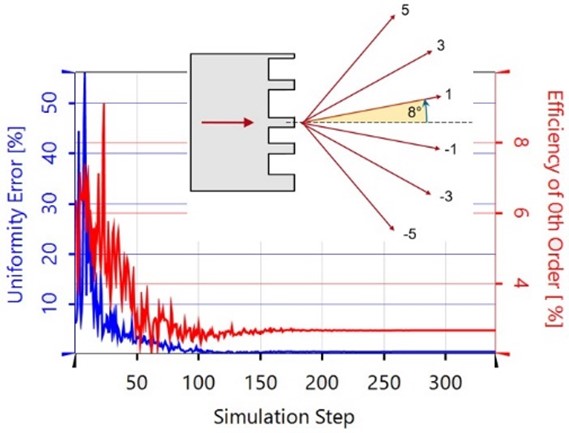
在這個用例中,我們演示了兩種具有不同配置目標和約束的優化:
在優化#1中,優先考慮均勻性誤差。
在優化#2中,0級也要最小化。

關于評價函數約束,用戶可以指定
單獨的目標值、范圍、下限或上限是什么
以及通過權重,它們的貢獻應該是什么。
在優化過程中,采用了內建的下降單純形算法
評價函數約束的配置
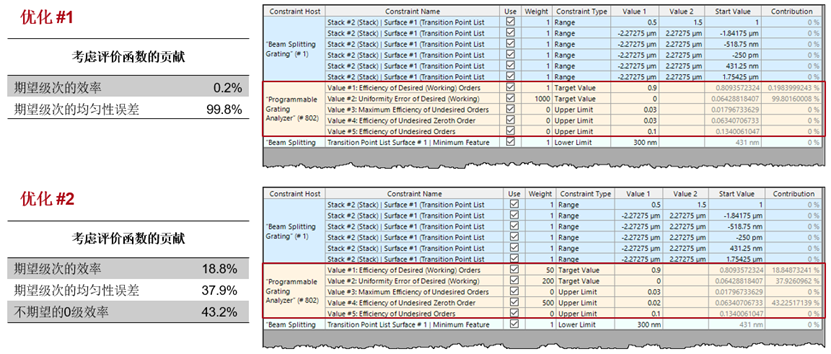
優化#1(優先級=均勻性誤差)
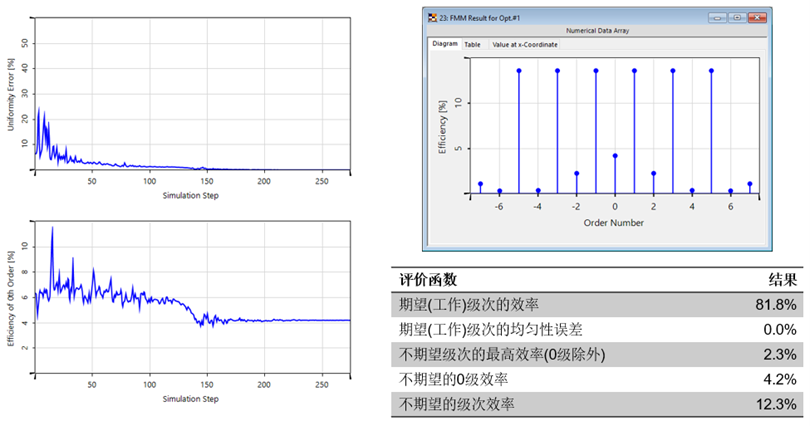
優化#2(優先級=均勻性誤差&低0級)
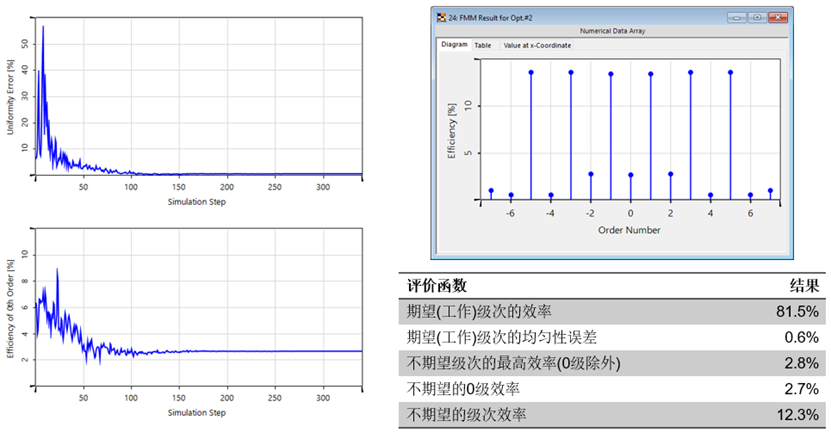
嚴格結果對比(初始—優化#1—優化#2)
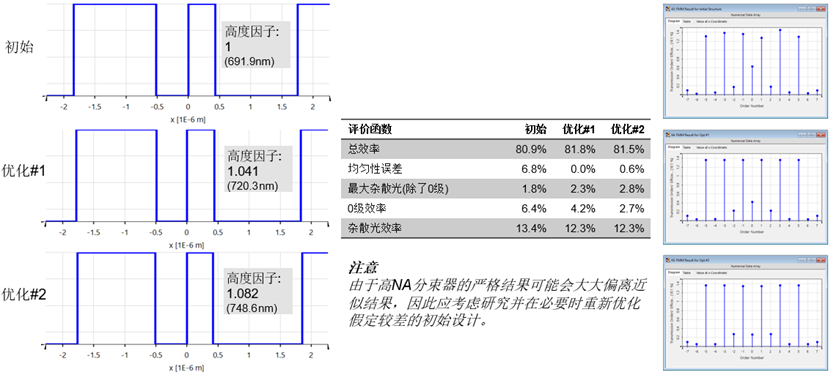
公差仿真結果
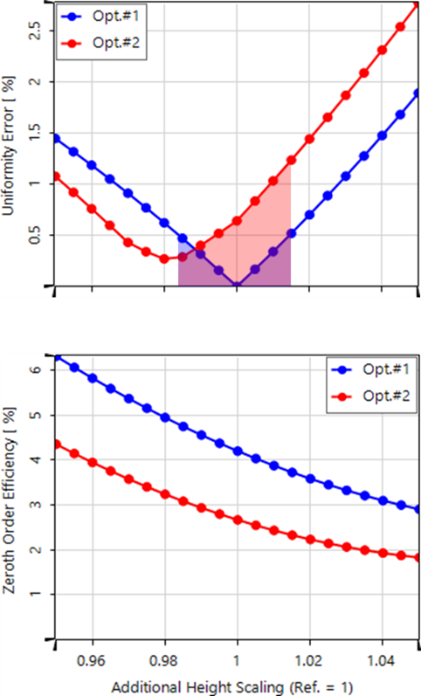
研究了在±5%范圍內生產過程中可能的高度公差時質量函數的表現。
在大部分的公差范圍內,蝕刻深度誤差約為±1.5%(藍色&紅色區域長度),第二種優化設計的均勻性明顯較差。
乍一看,優化#2的最小均勻性誤差(紅色曲線@0%)并不居中,這似乎有些奇怪。這是因為優化#2優先考慮了低0級效率,從而犧牲了一些均勻性來實現這一目標。
因此,對于公差分析的整個預期范圍,第2種優化的結構總是有一個明顯較低的0階。
注意:
公差仿真結果中的參考值1總是指被檢測結構的各自單獨優化高度(用紫色線表示)。
公差仿真結論
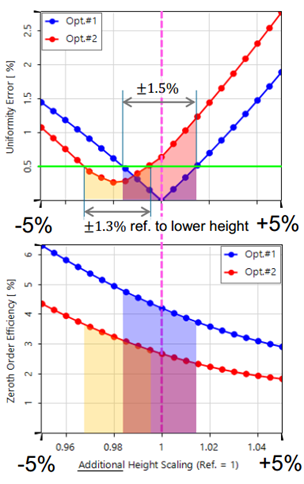
公差測試提供了一個更好的信息基礎,以決定什么是最適合所需應用的結構。
可以看出,如果使用均勻度誤差最低的高度,在相似的±1.3%(黃色區域長度)的公差范圍內,第2次優化的結構均勻度誤差低于0.5%(綠線)。
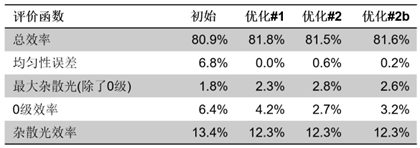
因此,具有 0.9825 (707.7 nm) 額外高度縮放的第二次優化結果可能是一個具有整體性能合適的良好解決方案。在下表的最后一列“優化#2b”中顯示了相應的結果。
文件信息

延伸閱讀
- 可編程光柵分析器
- 非近軸衍射分束器的設計與嚴格分析
- 產生二維光標的衍射分束器的設計
|