我們提出了一種處理傅里葉變換的方法,其并不需要二次多項式相位項的抽樣,而是用解析的方法處理。我們提出該理論的同時也給出了幾個例子證明其潛力。
1.簡介
物理光學建模需要頻繁地從空間轉換到角頻域,反之亦然。這可以由電場和磁場分量的傅里葉變換得到。所以,快速傅里葉變換(FFT)算法成了快速物理光學建模的支柱[1]。FFT技術的數值計算量與場分量復振幅所需采樣點的數量近似成線性關系。在光學中,我們經常處理有強波陣面相位的場分量,例如:球形。但是由于2π模,平滑的波陣面相位的復抽樣導致了大量的數值計算工作,甚至在FFT中也是如此。
2.理論
2.1 場的表征:提取二次相位
我們從空間域的符號開始,在本文中我們使用符號 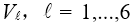 對應6個場分量,也就是V = (E, H):
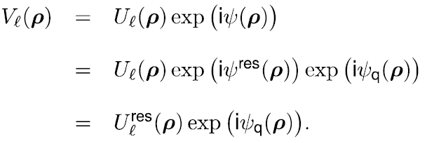 (1)
在公式1中,我們假設場 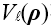 有兩部分:衍射場 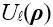 和一個平滑的波陣面相位exp(iψ(ρ))。對于得到的結果,我們從波陣面相位中提取二次相位exp(iψ(ρ))并且將余下的部分認為是余項場 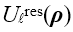 。假設exp(iψ(ρ))可由其實數系數C和D = (Dx, Dy)給出:
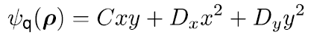 (2)
顯然,在強二次相位情況中,全場 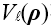 比余項場需要更多的抽樣量。所以,我們的目標是通過FFT且無二次相位項exp(iψ(ρ))抽樣的情況下,計算V(ρ)的傅里葉變換。
2.2.半解析傅里葉變換
從卷積定理可知:
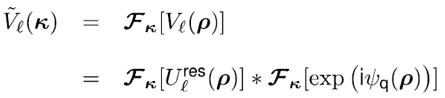 (3)
通常來說,項 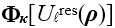 必須進行數值計算處理。另一方面,從數學角度[2]我們可知:
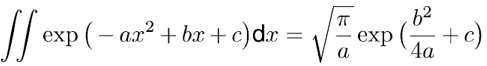 (4)
適用于任何復 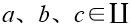 ,只要R{a} ≥ 0且a ≠ 0。
在該數學工具的幫助下,項κ[exp(iψ(ρ))]的解析表征可以推導出來:
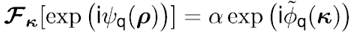 (5)
其中:
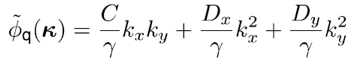 (6)
其中常數項 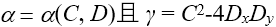 。
將公式5帶入公式3,通過改變卷積和傅里葉變換積分的階次,我們發現 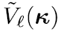 可以表示為:
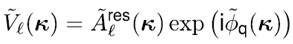 (7)
其中:
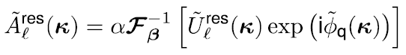 (8)
這里, 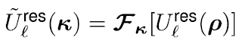 和坐標項 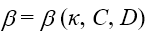 。公式7-8是半解析傅里葉變換的數學表達式。它表示全場的FFT可被兩個余項場的FFT替代。
3.數值仿真
這些概念在物理光學建模和設計軟件Wyrowski VirtualLab Fusion[3]中實現。
3.1.有效性測試1:純二次相位
在第一組測試中,我們準備了余項場 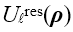 ,其幅度信息如圖1所示,且相位為零。我們將不同的二次相位項exp(iψq(ρ))與之相乘,組成 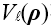 。然后我們分別對全場 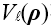 應用FFT和半解析FFT。
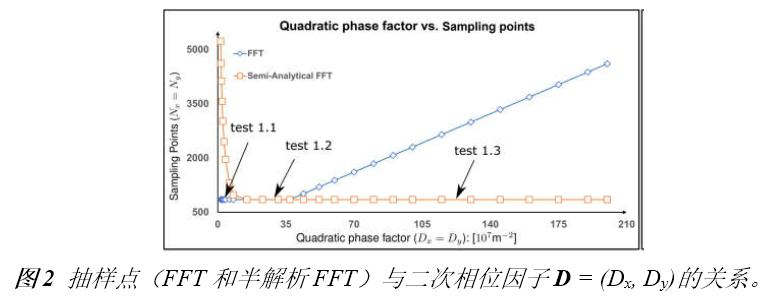
圖2展示了不同情況下FFT和半解析FFT所需的采樣點。可以發現當場有強二次相位時,半解析FFT需要比FFT少得多的抽樣點。
在圖3中我們給出了三個典型位置的角頻譜的振幅。解釋了波陣面相位的物理意義,因此當波陣面相位非常小時,在FT中衍射效應占主導地位。否則,當波陣面相位增加時,FT展現了越來越多的幾何特征。
3.2 有效性測試2:球形相位
在第二組中,我們將乘上另一種相位:球形相位 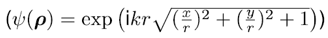 。
不像測試1,我們只能用解析方法處理二次部分而不能處理整個球形相位。所以,余項場的相位不再是零而是球形和二次相位之間的差值,并且它會隨著球半徑r的減小而越來越大。
不同情況下FFT和半解析FFT的抽樣點于圖4給出。結果顯示在強球形相位情況下,由于相位差, 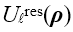 需要更多的抽樣點,這導致了半解析FT的抽樣數量同樣增加了。
4.結論
我們論證了半解析FFT的推導并且展示了幾個數值例子。事實表明,半解析FFT的采樣僅取決于余項場。在波陣面相位較強的場中,半解析FFT需要的采樣點明顯較少。
參考文獻
[1] E. O. Brigham, “The fast Fourier transform and its applications.” (1988).
[2] L. Mandel and E. Wolf, Optical coherence and quantum optics (Cambridge university press, 1995).
[3] “Wyrowski VirtualLab Fusion, developed by Wyrowski Photonics UG, distributed by LightTrans GmbH,”.
|


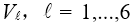 對應6個場分量,也就是V = (E, H):
對應6個場分量,也就是V = (E, H):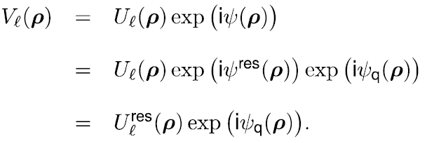 (1)
(1)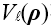 有兩部分:衍射場
有兩部分:衍射場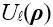 和一個平滑的波陣面相位exp(iψ(ρ))。對于得到的結果,我們從波陣面相位中提取二次相位exp(iψ(ρ))并且將余下的部分認為是余項場
和一個平滑的波陣面相位exp(iψ(ρ))。對于得到的結果,我們從波陣面相位中提取二次相位exp(iψ(ρ))并且將余下的部分認為是余項場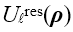 。假設exp(iψ(ρ))可由其實數系數C和D = (Dx, Dy)給出:
。假設exp(iψ(ρ))可由其實數系數C和D = (Dx, Dy)給出: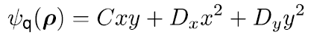 (2)
(2)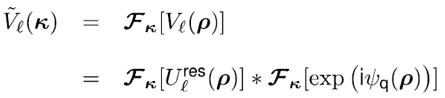 (3)
(3)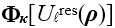 必須進行數值計算處理。另一方面,從數學角度[2]我們可知:
必須進行數值計算處理。另一方面,從數學角度[2]我們可知: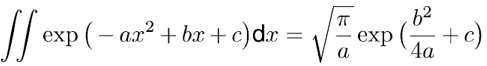 (4)
(4)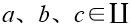 ,只要R{a} ≥ 0且a ≠ 0。
,只要R{a} ≥ 0且a ≠ 0。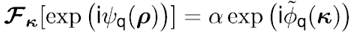 (5)
(5)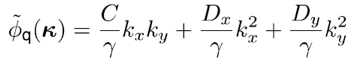 (6)
(6)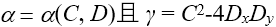 。
。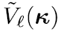 可以表示為:
可以表示為: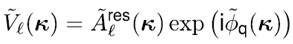 (7)
(7)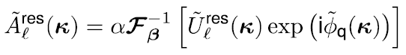 (8)
(8)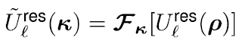 和坐標項
和坐標項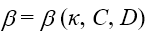 。公式7-8是半解析傅里葉變換的數學表達式。它表示全場的FFT可被兩個余項場的FFT替代。
。公式7-8是半解析傅里葉變換的數學表達式。它表示全場的FFT可被兩個余項場的FFT替代。

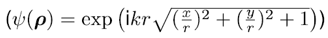 。
。