摘要
光柵結構廣泛用于光譜儀,近眼顯示系統等多種光學系統。VirtualLab Fusion通過應用傅立葉模態法(FMM),以簡易的方式提供對任意光柵結構進行嚴格分析。在光柵工具箱中,可以在堆棧中使用界面或/和介質來配置周期性結構。 用于設置堆棧幾何形狀的用戶界面非常人性化,并且允許生成更復雜的光柵。在該用例中,討論了由FMM實現衍射級次偏振狀態的研究。
概述
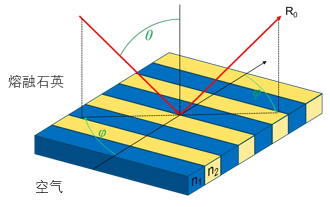
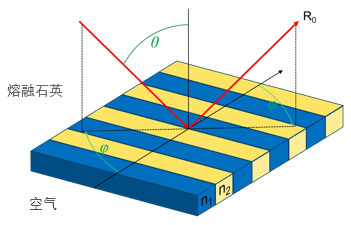
•本文的主題是光在周期性微結構處的衍射后的偏振態。
•為此,如示意圖所示,在示例性二元光柵結構和錐形入射處研究零級反射光。
•為了在特定示例中討論該主題,在第二部分中根據Passilly等人的工作(2008年)選擇光柵配置和相應參數。
衍射級次的效率和偏振
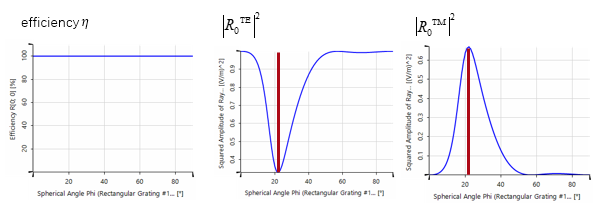
•通常,為了表征光柵的性能,給出了傳播級次的效率(η)。
•該效率值包括該特定級次的所有光的能量,但并不區分最終出現的不同偏振狀態。
•在嚴格模擬光柵效率的過程中,例如利用傅里葉模態法,通過使用復數場求解均勻介質的波動方程(也稱為亥姆霍茲方程)。
•因此,對于每個衍射級次(𝑛)和偏振態,算法的結果以復數值瑞利系數給出。
•特定級次(𝑛)的效率表示入射光的功率與輸出衍射級的光功率之間的關系。它是從瑞利系數計算出來的。
光柵結構參數
•此處探討的是矩形光柵結構。
•為簡單起見,選擇光柵的配置,僅使反射中的零級次(R0)傳播光線。
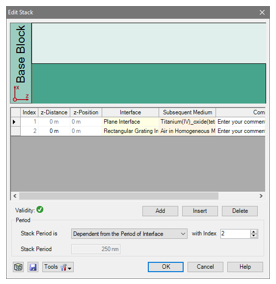
•因此,選擇以下光柵參數:
- 光柵周期:250 nm
- 填充系數:0.5
- 光柵高度:200 nm
- 材料n1:熔融石英
- 材料n2:TiO2(來自目錄)
偏振狀態分析
•使用不同錐形入射角(φ)的TE偏振光照射光柵。
•如上所述,瑞利系數的平方幅值將提供有關特定級次的偏振狀態信息。
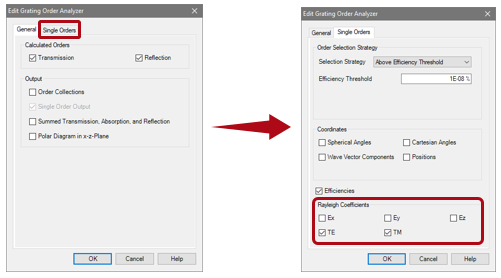
•為了得到瑞利系數,請在光柵級次分析器中選中單個級次輸出,并選擇所需的系數。
產生的極化狀態
其他例子
•為了不同狀態之間接收高轉換,在Passilly等人的工作中,研究和優化了在亞波長光柵處衍射光的偏振態。
•因此他們將模擬結果與制造樣品的測量數據進行了比較。
光柵結構參數
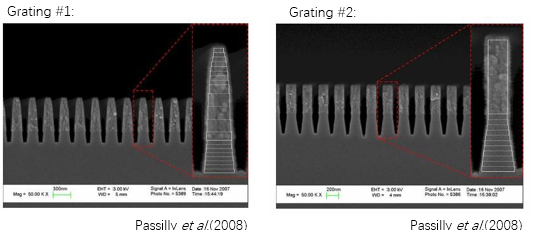
•在引用的工作中,研究了兩種不同的制造光柵結構。
•由于應用的制造方法引起的,與所需的二元形狀相比,結構表現出一些偏差:基板的蝕刻不足和光柵脊的形狀偏離。
•由于缺少有關制造結構的細節,因此在VirtualLab中的模擬,我們進行了簡化。
•當然,如果數據可用,詳細分析光柵的復雜形狀亦是可能。
光柵#1
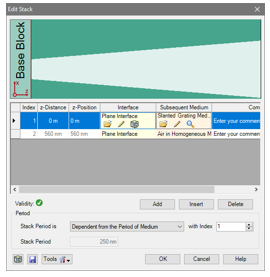
•僅考慮此光柵。
•假設側壁表現出線性斜率。
•蝕刻不足的部分基板被忽略了。
•為了實現光柵脊的梯形形狀,應用了傾斜的光柵介質。
假設光柵參數:
•光柵周期:250 nm
•光柵高度:660 nm
•填充系數:0.75(底部)
•側壁角度:±6°
•n1:1.46
•n2:2.08
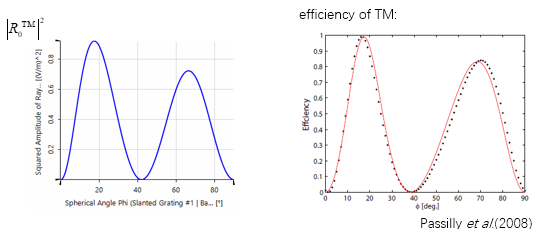
光柵#1結果
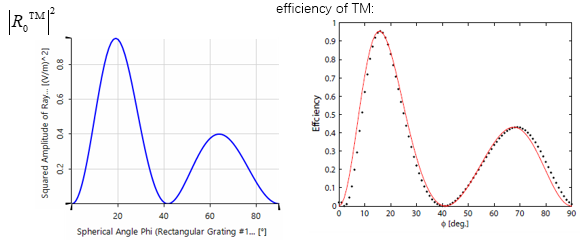
•左圖顯示的是使用VirtualLab獲得的結果,而Passilly等人發表的結果如右圖所示。
•相比之下,這兩張圖都表現出非常好的相似性,尤其是圖的軌跡。
•與參考相比,光柵結構的簡化導致了一些小的偏差。 由于缺少復雜光柵結構的數據,因此簡化是必要的。
光柵#2
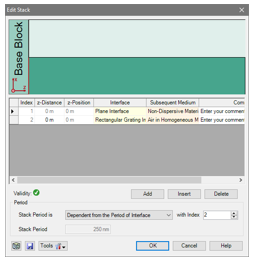
•同樣,只考慮此光柵。
•假設光柵有一個矩形的形狀。
•蝕刻不足的部分基板被忽略了。
假設光柵參數:
•光柵周期:250 nm
•光柵高度:490 nm
•填充因子:0.5
•n1:1.46
•n2:2.08
光柵#2結果
•同樣,左邊的圖顯示了使用VirtualLab獲得的結果,由Passilly等人發表的結果如右圖所示。
•相比之下,這兩張圖再次表現出非常好的匹配,尤其是圖的軌跡。
•與參考相比,光柵結構的簡化以及缺少一些光柵參數會導致一些小的偏差。
文件信息

|